The experience that I had on Semester at Sea was brought to life by the amazing crew, faculty, and students on board. All the people I’ve met and all the things I’ve seen and learned during my voyage has changed my life. I will be forever grateful for the semester I decided to study on a floating campus and have the world as my classroom.
the world isYOUR CAMPUS
Discover a global perspective for the challenges of tomorrow with a study abroad experience like no other.
Set Sail on the World’s Most Unique Floating College
Semester at Sea’s passenger ship brings together college students with learners at all stages of life to study with world-renowned professors in a shipboard classroom setting and in countries around the globe. With the ship as your home, you’ll find adventure, community, and life-changing experiences everywhere you go.
Check us out on Amazon Prime’s The College Tour
The Amazon Prime series tells the story of colleges and universities through the eyes of 10 hosts who share their unique perspectives on everything from campus life to academics, housing, athletics, and more. The College Tour produced a 30-minute episode about 10 voyager stories highlighting the Semester at Sea experience for traditional, gap-year, recent-college-graduate and international students, Lifelong Learners, and faculty.
What Is Semester at Sea?

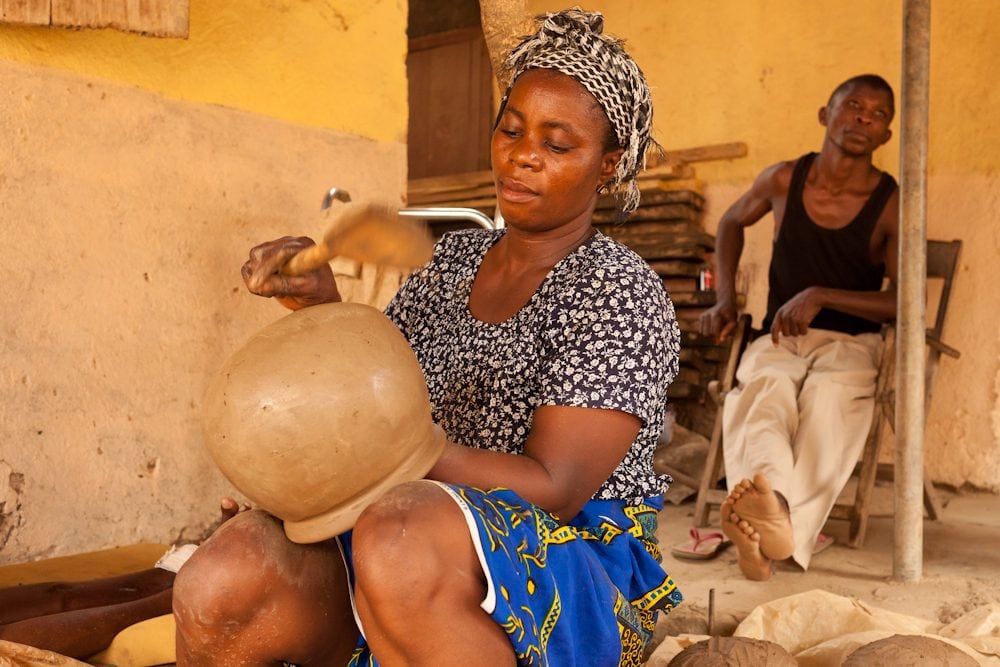






Become a Citizen of the World
Unlike traditional study abroad or tourism experiences, Semester at Sea opens the door to deep, authentic engagement with countries and cultures across the globe. It’s more than just the adventure of a lifetime. It’s a transformative experience that will give you a global perspective to take on the challenges of tomorrow.

September 09 — December 22
Ghana Hong Kong India Mauritius Morocco Mozambique Netherlands Portugal South Africa Thailand Vietnam

January 05 — April 20
Germany Ghana India Kenya Malaysia Morocco Mozambique South Africa Spain Thailand Vietnam
Who is Semester at Sea for?
Gap Year Students
Undergraduate Students
Recent College Graduates
Lifelong Learners
Faculty & Staff
The Semester at Sea Difference
Building true global understanding with a unique combination of academic rigor, immersive in-port experiences, and a transformative shipboard culture.
Top academic leaders share their knowledge through in-class and hands-on curriculum.
Immerse yourself in cultures around the world through academic Field Classes, structured Field Programs, or plan your own travel.
Build relationships that last a lifetime as part of a diverse community of learners.
Semester at Sea in Action
Voices from Our Voyagers
Recent News
-
 Fall 2025 AnnouncementsSemester at Sea announces the Fall 2025 Voyage itinerary
Fall 2025 AnnouncementsSemester at Sea announces the Fall 2025 Voyage itinerary -
 Spring 2024 Spring 2024Each voyage is life-changing and challenging, including this one.
Spring 2024 Spring 2024Each voyage is life-changing and challenging, including this one. -
 Fall 2024 Spring 2025 AnnouncementsSemester at Sea Day at CSU
Fall 2024 Spring 2025 AnnouncementsSemester at Sea Day at CSU